
100次浏览 发布时间:2024-08-16 13:17:57
证明线面垂直的方法一般有很多种,其中利用定义,判定定理和面面垂直的性质是最基本也是很重要的的方法,但是,有时这几种方法都不管用或者证明起来很困难,这时如果建立空间坐标系,使用空间向量法,说不定就会柳暗花明又一村。
(1)利用定义:如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面α互相垂直,记作l⊥α,直线l叫做平面α的垂线,平面α叫做直线l的垂面。如图,直线与平面垂直时,它们唯一公共点P叫做垂足。
符号表示:任意a⊂α,都有l⊥a=>l⊥α
(2)利用判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
符号表示:a⊂α,b⊂α,a∩b=P,l⊥a,l⊥b=>β∥α
(3)利用面面垂直的性质:两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,则这条直线与另一个平面垂直。
(4)空间向量法:即证明直线的向量与平面的法向量平行,就可以说明该直线与平面垂直。
用空间向量法证明线面垂直的方法和步骤为:
①建立空间直角坐标系
②将相关直线的方向向量用坐标表示
③找出平面内两条相交直线,并用坐标表示它们的方向向量;或求出平面的法向量
④分别计算所求直线与以上两相交直线向量的数量积,数量积都为0;或判断直线的方向向量与平面的法向量平行。
另外,还有:
(5)两条平行直线中的一条垂直与一个平面,那么另一直线也与此平面垂直;
(6)一条直线垂直与两个平行平面中的一个,那么这条直线也与另一平面垂直。

利用判定定理、面面垂直的性质
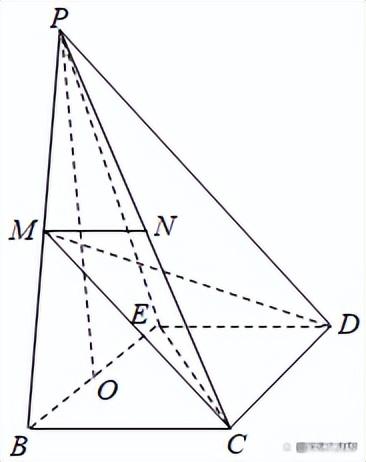
例1、(2019秋•赣州期末)在矩形ABCD中,AB=1,BC=2,E为AD的中点,如图1,将△ABE沿BE折起,使得点A到达点P的位置(如图2),且平面PBE⊥平面BCDE
(1)证明:PB⊥平面PEC;
(2)若M为PB的中点,N为PC的中点,求三棱锥M﹣CDN的体积.


空间向量法:
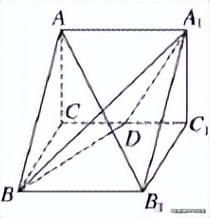
例2、如图所示,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1的中点,求证:AB1⊥A1BD。
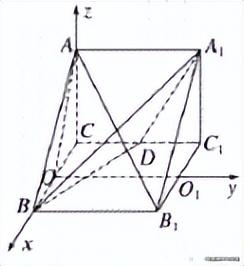
当然我们也可以找出平面内两条相交直线,并用坐标表示它们的方向向量,分别计算所求直线与这两条两相交直线向量的数量积,若数量积都为0,则说明线面垂直,各位同学可以自己亲手证明一下。