
100次浏览 发布时间:2024-08-18 09:04:10
七年级下学期数学,寒假预习,垂线的概念与性质,6个知识点。当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。

01知识点一:垂线的定义
例如:如图,AB、CD互相垂直,0叫垂足,AB叫CD的垂线,CD也叫AB的垂线。可记为: AB⊥CD,垂足为O,或AB⊥CD干点O。如果遇到线段与线段、线段与射线、射线与射线、线段与直线垂直时,特指它们所在的直线互相垂直。

∵∠AOD=90°(已知),∴AB⊥CD (垂直的定义)
∵AB⊥CD于点O(已知),∴∠AOD=∠AOC=∠BOC=∠BOD =90° (垂直的定义)
例题1:小红在学习垂线时遇到了这样一个问题,请你帮她解决:如图,线段AB和CD相交于点O,则下列条件中能说明AB⊥CD的是( )
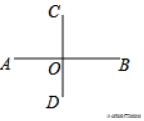
①∠AOD=90°; ②∠AOC=∠BOC:
③∠AOC=∠BOD; ④∠BOC+∠BOD=180°
⑤∠AOC+∠BOD=180°
分析:根据垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直进行判定即可。
解:①∠AOD=90°,可以得出AB⊥CD;②∠AOC=∠BOC,可以得出AB⊥CD:③∠AOC=∠BOD,不能得到AB⊥CD;④∠BOC+∠BOD=180°,不能得到AB⊥CD;⑤∠AOC+∠BOD=180°,可以得出AB⊥CD.故①②⑤共3个.

02知识点二:点到直线的距离
直线外一点到这条直线的垂线段的长度,叫作点到直线的距离。
例题2:下列语句中:①有公共顶点且相等的角是对顶角;②直线外一点到这条直线的垂线段,叫作点到直线的距离;③互为邻补角的两个角的平分线互相垂直;④经过一点有且只有一条直线与已知直线垂直.其中正确的个数有( )
解:①具有公共顶点,两边互为反向延长线的两个角为对顶角,故①不正确.
②直线外一点到这条直线的垂线段的长度,叫作点到直线的距离,故②不正确.
③互为邻补角的两个角的和为180°,那么互为邻补角的两个角的平分线互相垂直,故③正确.
④同一平面内,经过一点有且只有一条直线与已知直线垂直,故④不正确.
综上:正确的有③,共1个.
本题主要考查对顶角、点到直线的距离、邻补角、垂线,熟练掌握对顶角的定义、点到直线的距离、邻补角、垂线是解决本题的关键。

例题3:如图,P为直线l外一点,点A,B,C在直线l上,且PB⊥l,垂足为B,∠APC=90°,则下列语句错误( )
A.线段PB的长叫作点P到直线l的距离
B.线段AC的长叫作点C到直线AP的距离
C.PA、PB、PC三条线段中,PB是最短的
D.线段PA的长叫作点A到直线PC的距离
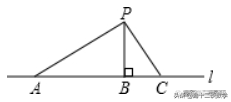
分析:根据“从直线外一点到这条直线的垂线段的长度,叫作点到直线的距离”和“从直线外一点到这条直线上各点所连的线段中,垂线段最短”进行判断,即可解答。
解:A、线段PB的长度叫作点P到直线l的距离,故原说法正确,故A选项不符合题意;
B、线段PC的长度叫作点C到直线AP的距离,故原说法错误,故A选项符合题意;
C、PA、PB、PC三条线段中,PB最短,故原说法正确,故C选项不符合题意;
D、线段PA的长叫作点A到直线PC的距离,故原说法正确,故D选项不符合题意.
03知识点三:垂线的画法
垂线的画法:
(1)放:放直尺,直尺的一边要与已知直线重合;
(2)靠:靠三角板,把三角板的一直角边靠在直尺上;
(3)移:移动三角板到己知点;
(4)画线:沿着三角板的另一直角边画出垂线。
例题4:下列各图中,过直线l外点P画l的垂线CD,三角板操作正确的是( )

解:根据垂线的作法,用直角三角板的一条直角边与l重合,另一条直角边过点P后沿直角边画直线即可,选D。

04知识点四:垂线的性质
过一点有且只有一条直线与已知直线垂直。
注意:过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线。
连接直线外一点与直线上各点的所有线段中,垂线段最短。
例题5:如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能正确解释这一现象的数学知识是( )
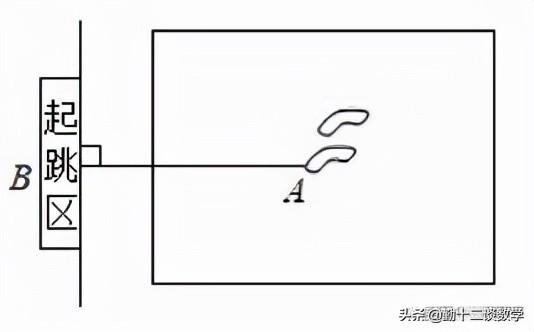
A.两点之间,线段最短
B.垂线段最短
C.两点确定一条直线
D.经过一点有且只有一条直线与已知直线垂直
解:如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能正确解释这一现象的数学知识是垂线段最短.
05角度的计算
例题6:如图:AB、CD、EF交于O点,AB⊥CD,OG平分∠AOE,∠COE=28°,求∠AOG的度数.

解:∵AB⊥CD,∴∠AOC=90°.
∵∠FOD与∠BOE是对顶角,
∴∠COE=∠FOD=28°,
∴∠BOE=90°-∠COE=62°,
∴∠AOE=180°-62°=118°,
∵OG平分∠AOE,
∴∠AOG=1/2∠AOE=1/2×118°=59°.