
100次浏览 发布时间:2024-08-10 08:04:29

它可能看起来并不重要,但我们必须了解它的工作方式,这样我们才能成为一个更好的程序员。
在计算时间复杂度和空间复杂度(通常用 Big-O 表示法表示)时,这里需要遵循几个规则:
时间复杂度
时间复杂度是算法运行所花费的时间量,它是输入长度的函数。 它测量执行算法中每个代码语句所花费的时间。
第一个例子
function add(x: number, y: number): number { return x + y;}上述函数的时间复杂度为 O(1),因为无论参数(输入)是多少,它总是运行一次指令。
这个功能怎么样? (包含for循环)
function double(numbers: number[]): number {
var sum:number = 0;
for (const number of numbers) {
sum += number;
}
return sum / numbers.length;
}函数 double 的时间复杂度是 O(n),因为循环的数量取决于传递给函数的数组的长度。
这个功能怎么样? (包含嵌套的 for 循环)
function(n: number): number {
var count:number = 0; for (let i = 0; i <= n; i++) {
for (let j = 0; j <= i; j++) {
count++;
}
}
return count;
}count++ 以任意 n 值运行多少次?
所以 count++ 会运行……
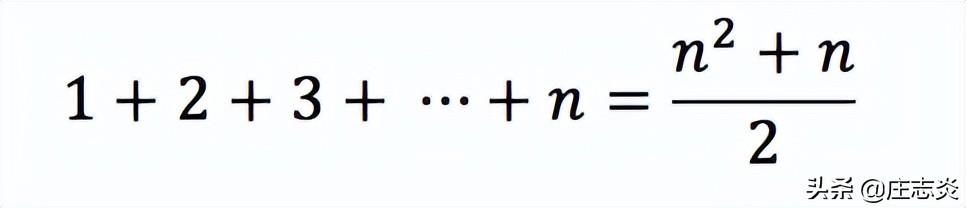
时间复杂度将是 O(n²),记住我之前告诉你的规则。
现在让我们尝试多一点代码(包含 3 个 for 循环)。
someFunction function(a: number[], b: number[]): number {
var x:number = 0;
var y:number = 1; for (let i = 0; i < a.length; i++){
x += a[i];
} for (let j = 0; j < b.length; j++){
y *= b[j];
} for (let k = 0; k < 10; k++){
y += 1;
x -= 1;
}
return x + y;
}假设数组 a 的长度是 N ,数组 b 的长度是 M ,时间复杂度可以这样确定:
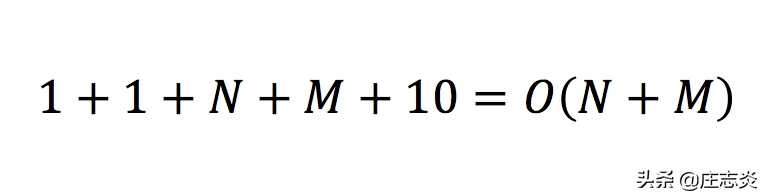
等一下,循环 for (let k = 0; k < 10; k++) 的复杂度是 O(1),因为它将运行 10 次(常数)。
所以 someFunction 的时间复杂度是 O(N+M) 或者如果我们确定数组 a 和 b 的长度都是 N,它将是 O(2N)。
空间复杂度
空间复杂度是指算法/程序使用的内存空间总量,包括用于执行的输入值空间。
例如
function add(x: number, y: number): number { return x + y;}这个函数需要2个单位的空间(2个参数x和y),当这个函数运行时,这个内存空间分配将保持不变,不管输入如何,所以空间复杂度是O(1)。
第二
sum += number;
}
return sum / numbers.length;
}此函数需要 N 个空间单位(任意数量的参数号)和 1 个空间单位用于变量求和。 空间复杂度为 O(n),因为此函数将需要至少 N 个内存单元空间,具体取决于数组的长度。
综上所述
时间复杂度根据给定的输入确定算法在运行时运行多长时间,空间复杂度确定算法在运行时占用多少内存空间。

sacon空调用户售后客服中心实时反馈-今-日-汇-总(sacon空调空调制冷一点时间后跳闸 )
2025-08-28 17:57:48
远大中央空调各24小时售后全国客服受理中心实时反馈-今-日-汇-总(远大中央空调空调不制冷 )
2025-08-28 17:55:39
韩电空调售后服务号码—全国统一客服热线实时反馈-今-日-更-新(韩电空调空调好吗 )
2025-08-28 17:53:38
Carrier开利中央空调售后24小时联系方式维修查询实时反馈-今-日-资-讯(Carrier开利中央空调空调自动关机 )
2025-08-28 17:52:56
奥克斯(AUX)天花机客服号码售后号码大全及维修网点查询实时反馈-今-日-资-讯(奥克斯(AUX)天花机空调怎么显示温度 )
2025-08-28 17:52:34